 |
Maximaを使って、数式をフーリエ解析して、グラフ出力してみます。 なお、Maximaの使い方については、Maxima入門 Maximaのインストールから簡単な数式、グラフ作成までに入門向けに書かれています。  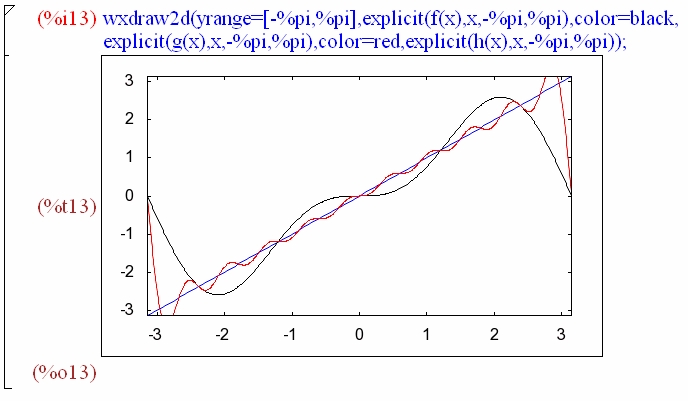 数式f(x)=xのグラフは、上図の青線です。 黒線がf(x)の第2項までのフーリエ級数で、赤線が第10項までのフーリエ級数で、項数を増やすと、 だんだんよくf(x)近似されるのが分かります。 maximaを使うと、このように簡単にフーリエ解析もできます。 なお、標準ではフーリエ解析できないので、fourieパッケージを読み込む必要があります。 注意が必要なのは、パッケージ名はfourieですが、演算子はfourierで、「r」がつきます! Maxima(マキシマ)の数式グラフ出力機能を使って、カオスやフラクタル図形のグラフも描いてみました。  カオスを扱うには、はじめにdynamicsパッケージを読み込んでいます。 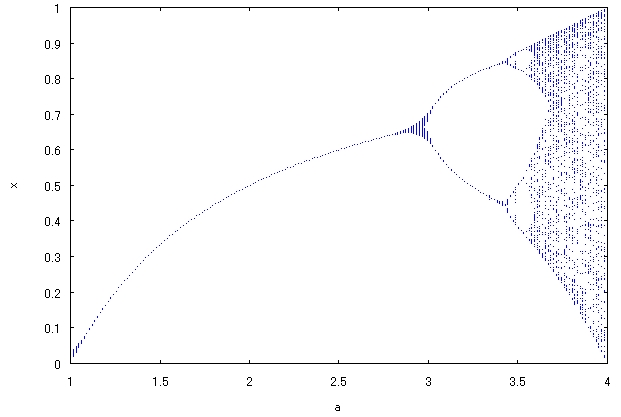 上図は有名なロジスティック写像です。 次に、フラクタルを3つ続けて描いてみます。  フラクタルは、fractalパッケージを読み込んだ後でグラフ出力します。 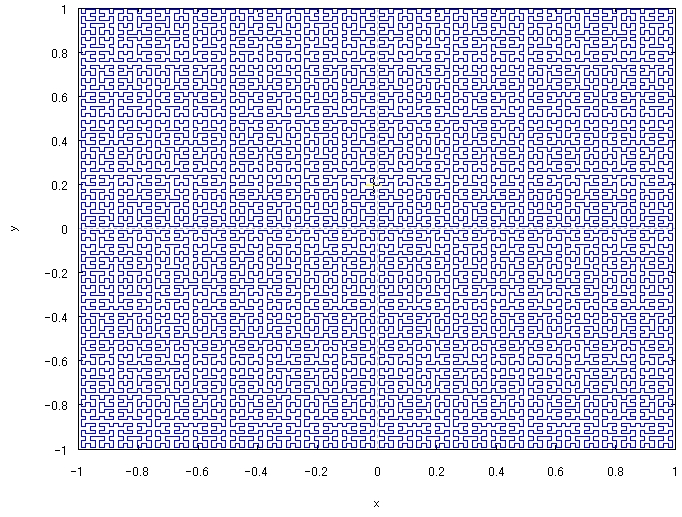 上図は、18式のHilbert写像です。 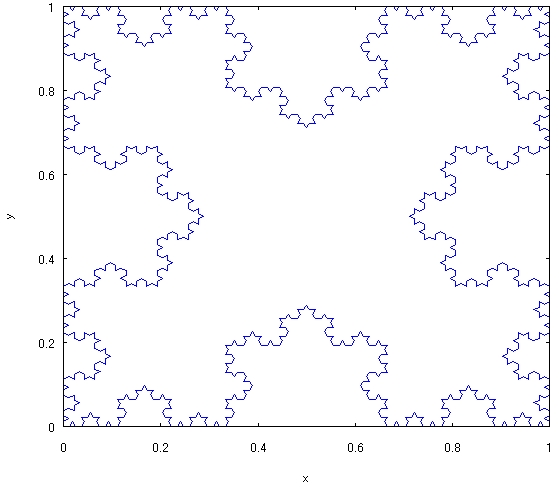 上図は、19式のKoch雪片集合です。 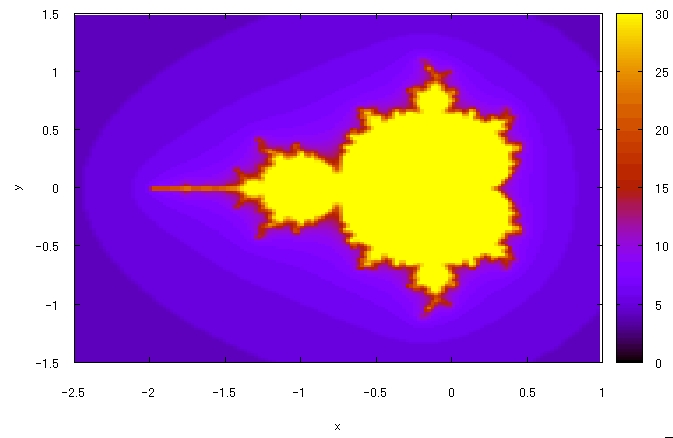 最後は、20式のMandelbrot集合です。 Maximaは、市販のMathematicaに劣らず有用なフリーの数式処理ソフトですので、 使いようによっては無限の可能性をひめています。 紹介した事項により生じた不都合などには責任は負えませんので、くれぐれも自己責任でお願いします。
|
| |
|||||
| Copyright (C) 2008, しおたに・ドット・チャイナ, All Rights Reserved. |